谷阿莫带你十分钟看完 NavMesh 生成算法

（本文配图皆来自《Crowds In A Polygon Soup: Next-Gen Path Planning》By David Miles, David Miles, David Miles, David Miles 与 《Study: Navigation Mesh Generation》By Stephen Pratt。“窃书不能算偷……窃书！……读书人的事，能算偷么？”）

大家好，我是谷阿莫，今天我给大家带来的是 NavMesh 的生成方法。

这个算法从一个二维的简化例子开始讲起。当我们谈寻路算法的时候，在二维世界中，我们谈的是这样一个问题：

如下图，左边有个走廊，中间是一个通道，右边是一个骷髅状的洞穴。起点在左，目标在右，如何找到一条最为合适的路径。

在这个例子中，我们似乎很难直接求解一个合适的路径。主要的问题时，我们掌握的数据并不是一个抽象的结构化的数据。

所以，首先，我们需要从问题中产生一个抽象的结构化的数据，用来简化问题求解。

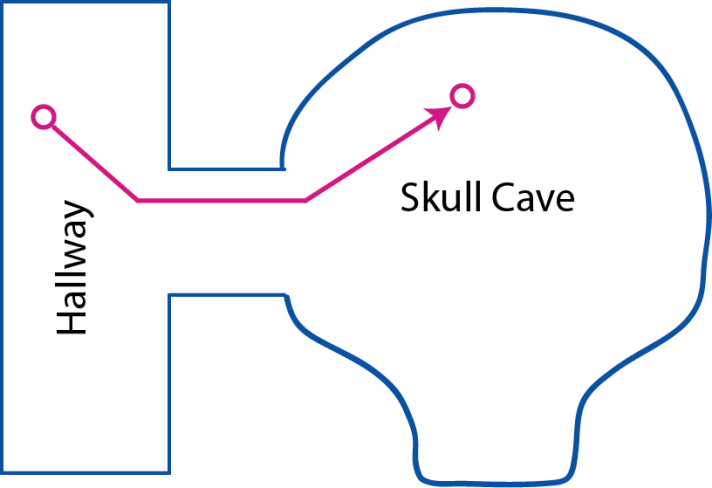
一个很朴素的思路，即是把地图数据栅格化（像素化）。在栅格化的地图上，至少可以通过搜索格子的方式（向周围四方向搜索或八方向）找到一条可行的路径，尽管很挫。

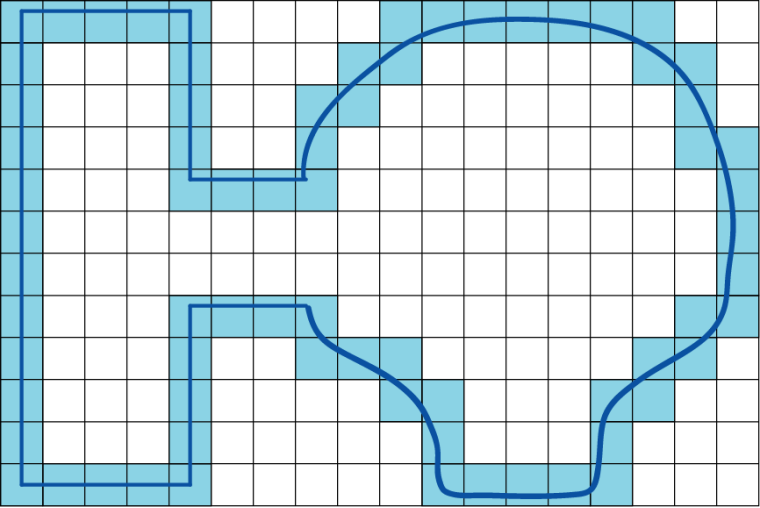
在栅格化的地图上做一个边缘提取，获得地图区域像素化后的内边缘，得到以下图形数据。

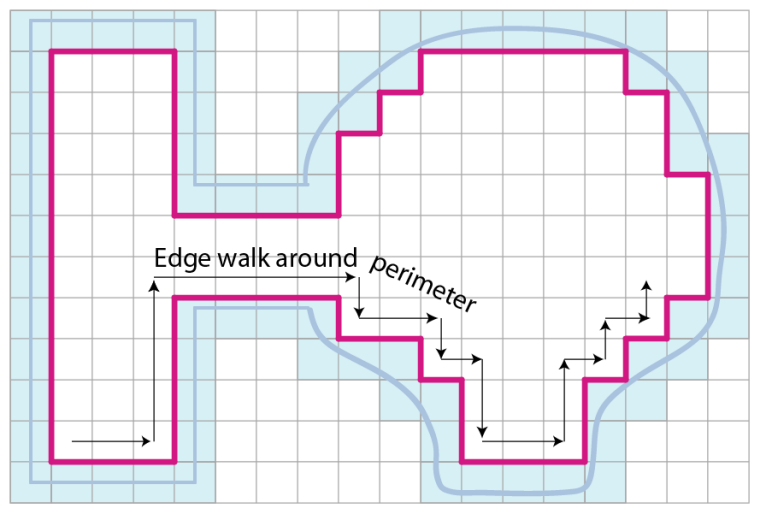
进一步，对锯齿化的边缘进行简化，得到一个简化的多边形地图区域。

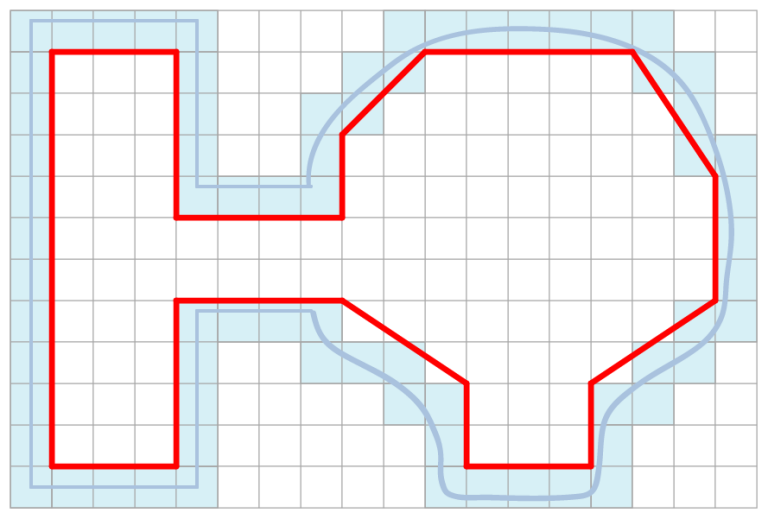
可以使用下述方法对锯齿化的边缘进行简化。 选择两个点进行连线可得到一条简化的边。

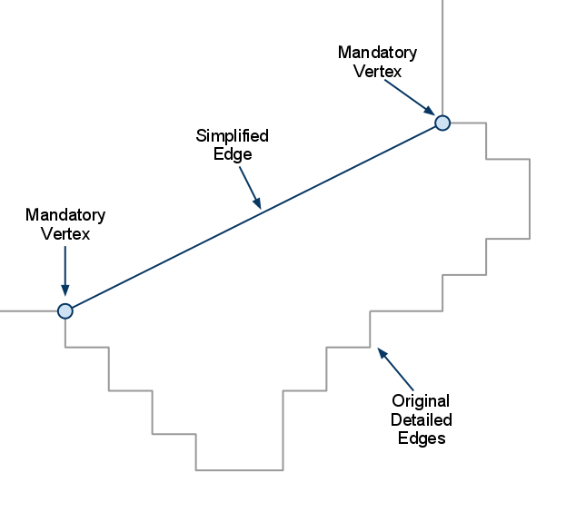
找到离该简化边缘距离最远的点，将该点加入简化多变形的轮廓集合中，此时将产生替代旧边缘的两条新的简化边缘。

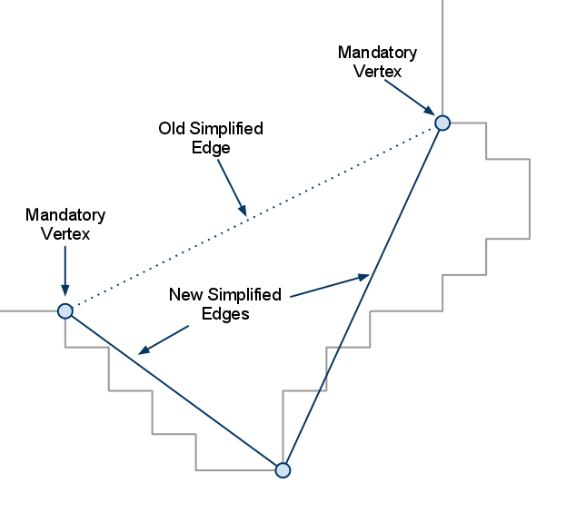
重复该过程，直到所有不在简化轮廓集合中的点距离简化的边缘距离都小于某阈值。

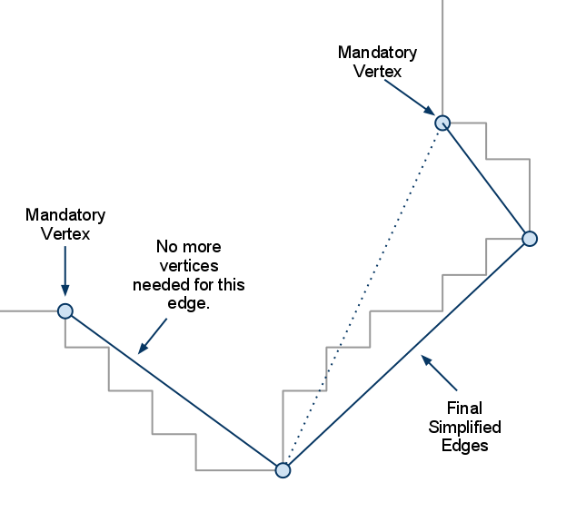
考虑到简化后的地图实际上很多存在很多可以直接通过直线联通的区域，我们可以进一步对这个地图做一个简单的划分。如下图，简化后的多边形地图区域可以分割为以下四个联通区域。

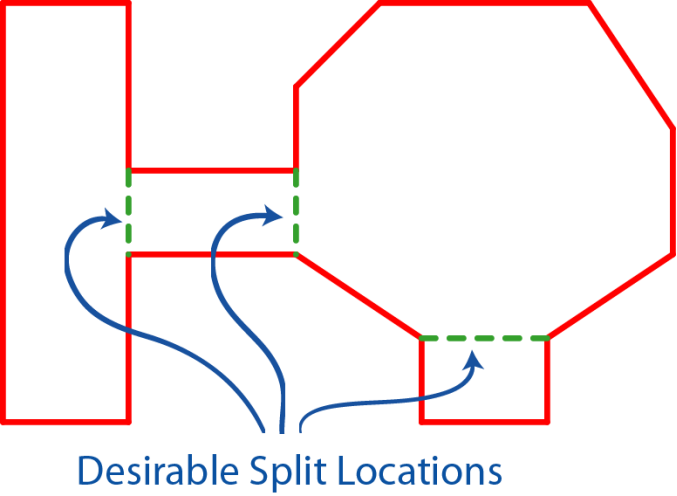
分割区域按照以下算法进行： 两点间直线距离/两点边界距离 为 度量，当该值小于一定阈值时，进行区域分割。

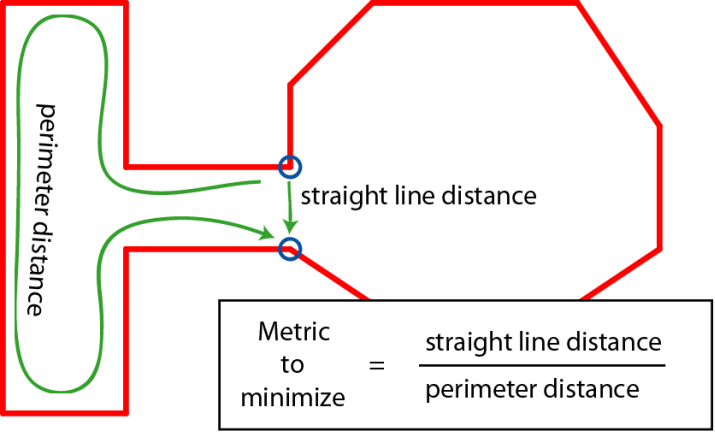
该过程可以以递归的方式进行，整个过程复杂度<=O(Log(n)*n)，n为地图边。

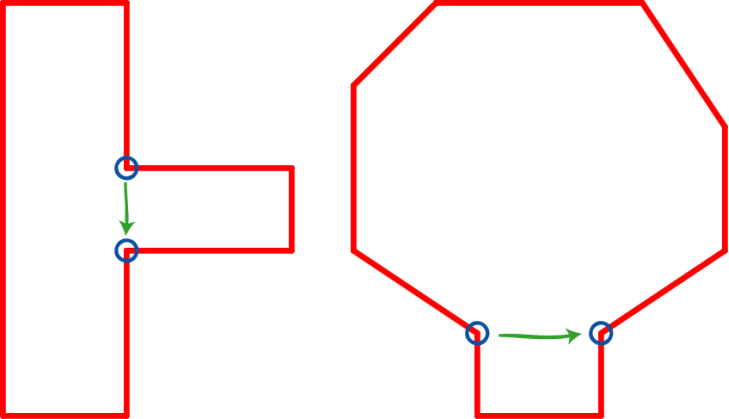
在完成区域分割后，我们可将整个地图数据视为一个图。即 左走廊 -> 中间通道 -> 右上洞穴区域 -> 右下洞穴区域。每个图节点区域中的两点都可以通过简单的直线路径相互连通。

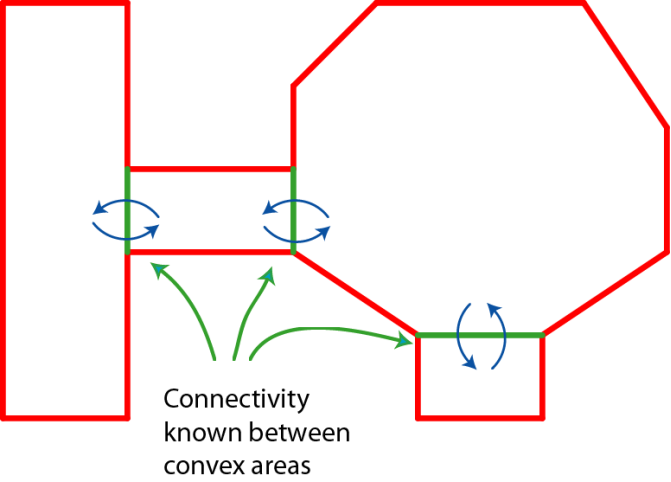
此时，我们可以用最短路径算法（如 Dijkstra ）来解决图节点间的寻路问题，而图节点内的路径可以简单的通过两点间连线完成。

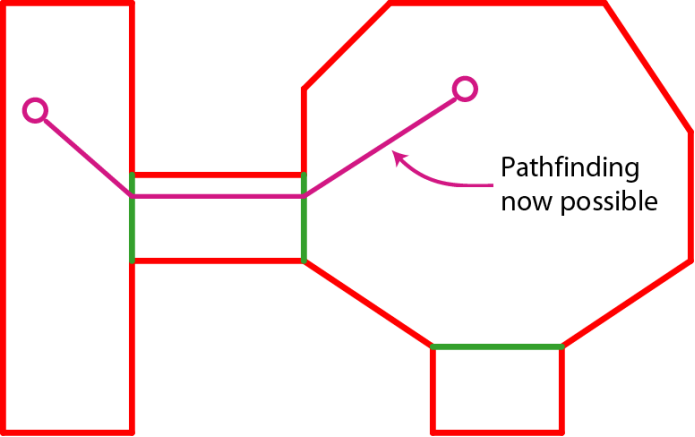
上面例子是一个最简单的地图形式，下面考虑地图中带空洞（不可行走）区域的情况。下图在右边骷髅状洞穴区域添加两个不可行走的空洞。我们希望算法能够生成如下图表示的寻路路径。

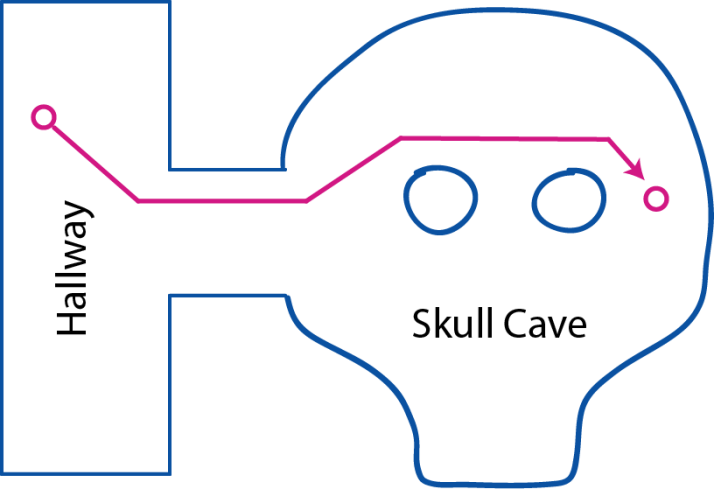
使用和上文描述相同的步骤对地图进行像素画、边缘提取、多边形简化，可以得到如下地图数据。对每个空洞区域， 找到其和地图边界点距离最小的点，将该两点的连线作为额外边界添加到地图中。

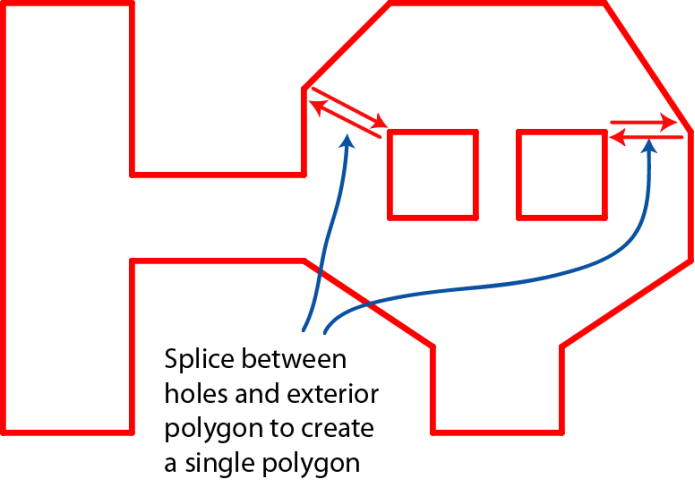
此时，地图退化为简单多边形（如下图所示），应用上述区域分割方法即可将地图进一步处理。

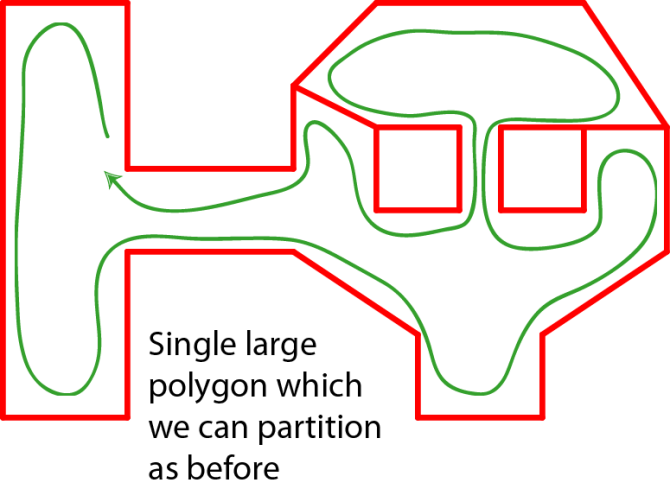
将地图抽象为如下联通区域图，即可在图上应用寻路算法。

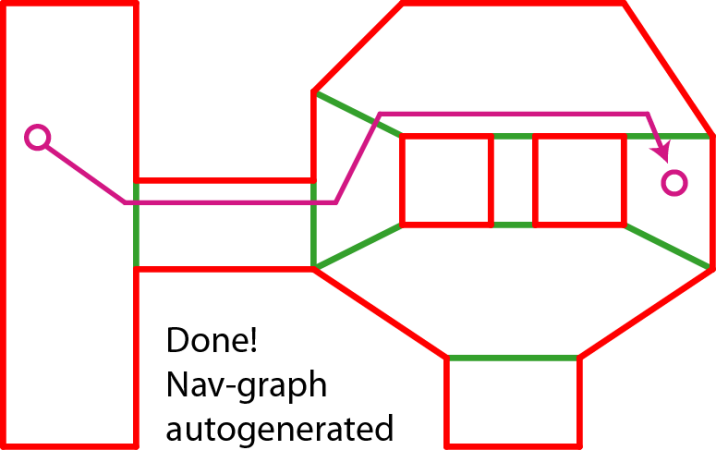
看一个三维空间上的例子，在3维空间中，我们需要将二维对地图数据的像素化过程变为对三维地图模型数据的体素化过程。

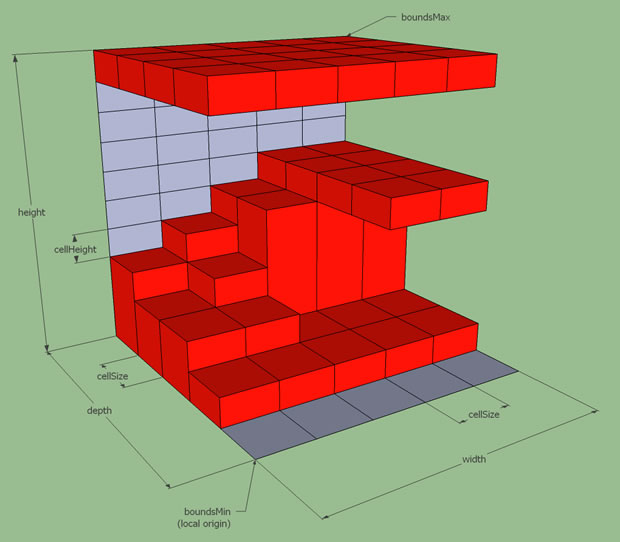
而事实上，在三维空间，模型数据表示的是不可进入的区域，在空间中，可以使用下图数据结构表示可行走的地图区域，每一个二维地图网格中存储一组由可行走区域上边界与下边界描述的数据。其中，可行走区域的下边界，即地板表面数据即是我们用来生成寻路网格的表面。

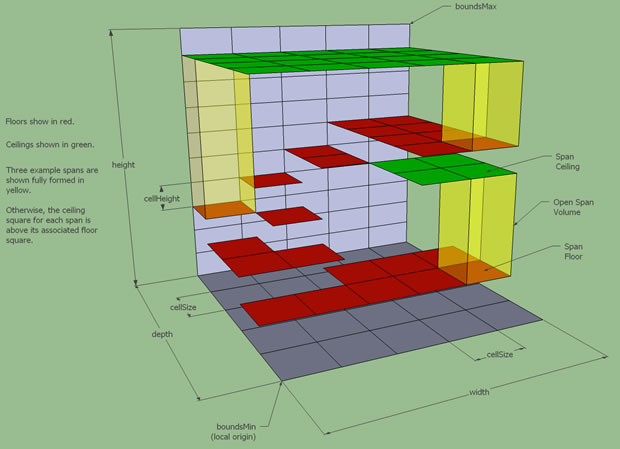
如下图所示，使用寻路角色身高可以对可行走区域进行剔除。

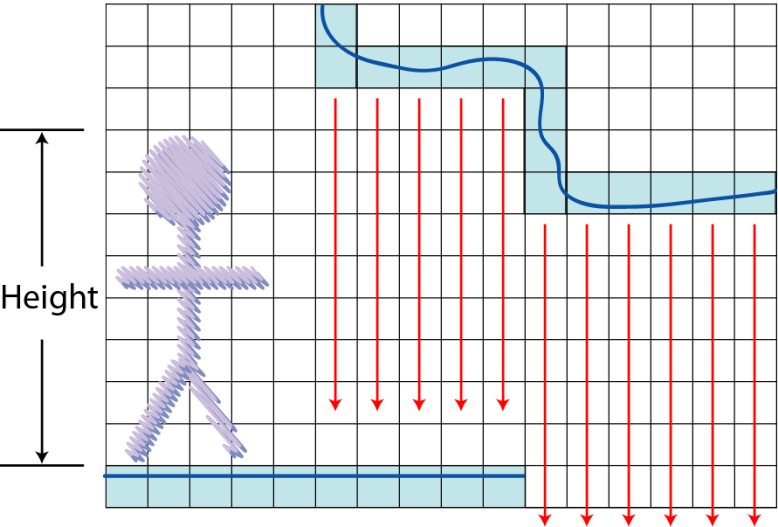
考虑一个在三维空间中可行区域存在重叠的情况（如下图，形如一个盘旋的楼梯区域）。

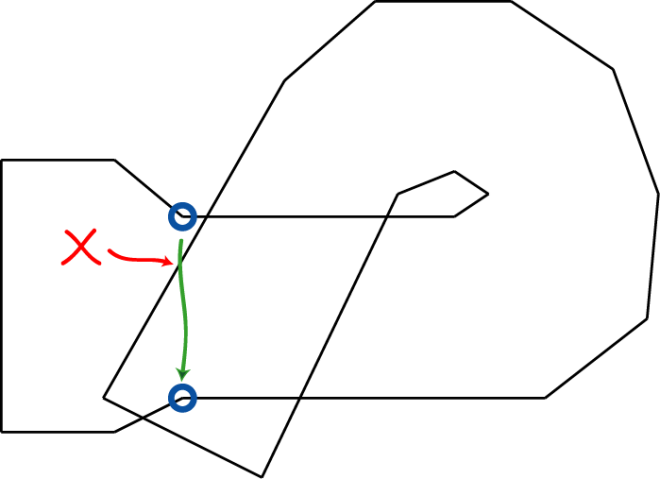
直接使用和上文二维例子描述中相同的区域分割算法进行区域分割。

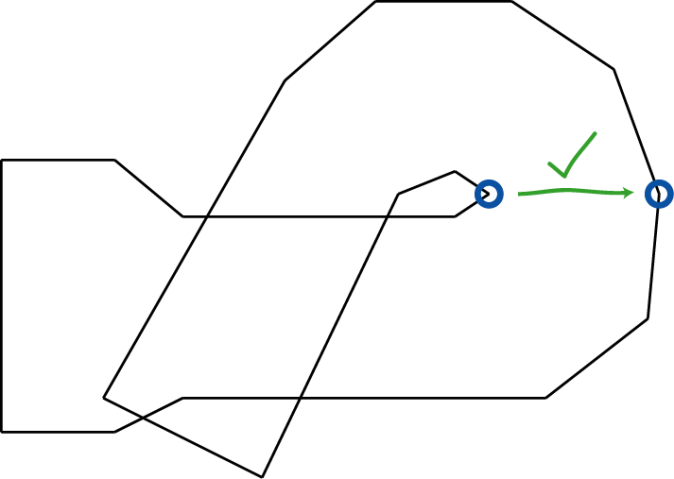
上图所示地图可被分割为如下所示无重叠的两部分区域，即三维空间中地图重叠部分可在区域分割过程中解决。可对该两区域继续递归进行处理，生成上文描述的寻路区域数据。

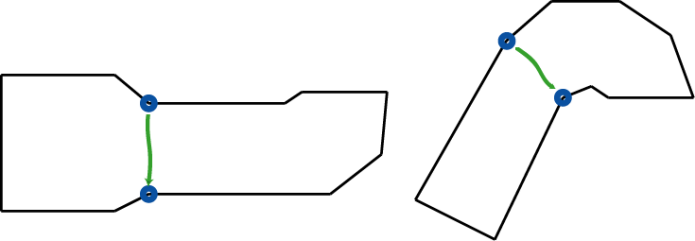
对于不同体型半径的，我们希望会生成不同的寻路路径，如下图例子所示，寻路角色体型半径过大无法通过中间连接区域，所以图中在上文生成的路径对体型半径过大的角色是不可行的。

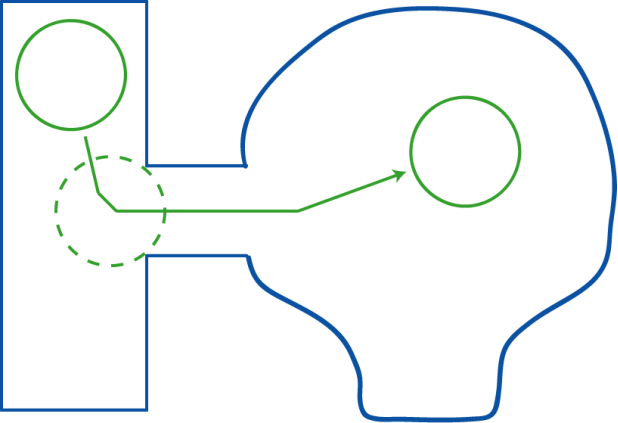
该问题可以在提取地图区域边缘时，向内多取一个角色体型半径生成特殊的寻路地图（即每种半径生成一个寻路网格）。同一地图数据，针对大体型角色，边缘提取过程后生成的寻路区域如下图所示。

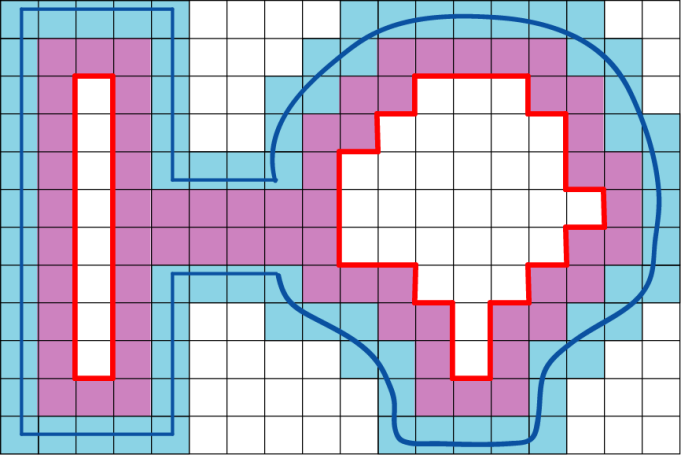
关于动态障碍，可采用在运行时改变寻路地图与动态障碍物重叠的节点数据完成，如下图所示，再添加动态障碍物前期望生成的寻路路径如左图，添加障碍物后期望生成的寻路路径如右图。

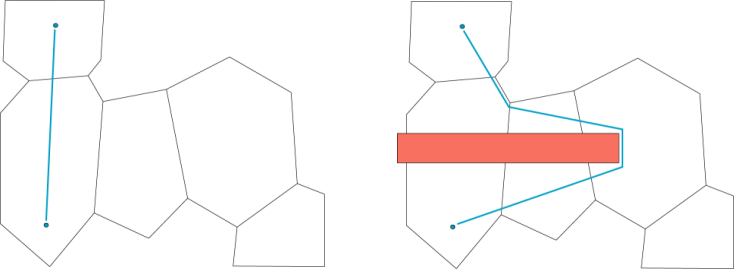
添加动态障碍物后，仅需在运行时替换与障碍物重叠的BCD节点，将其数据替换为B1B2C1C2D1D2D3节点，当障碍从地图中取出后再将界点恢复。

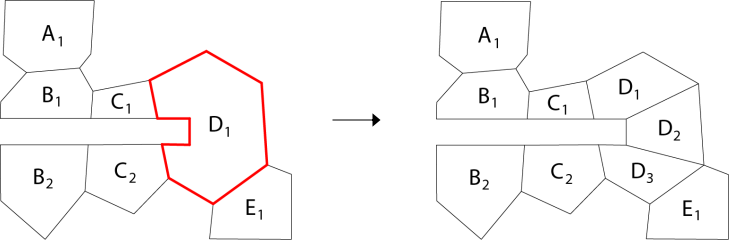
关于如何寻找寻路路径上的拐点。当路径跨多个联通区域时，可使用以下方法确定路径上的拐点。

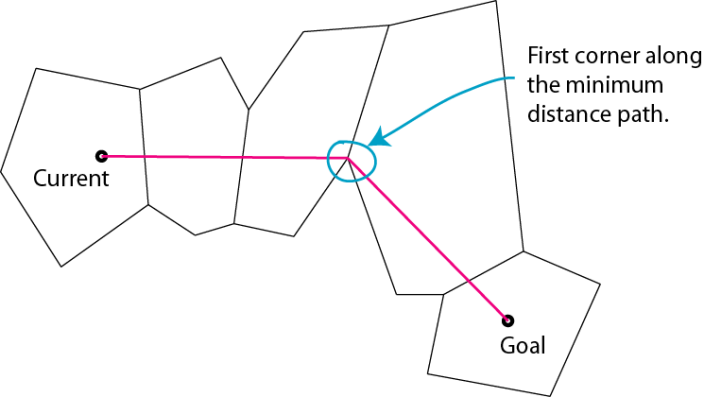
首先，确定路径上穿过的区域边缘。

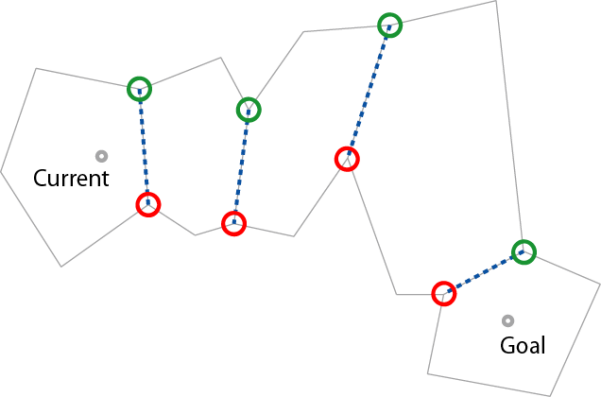
顺序遍历边缘，记录最右的左边缘点与最左的右边缘点。

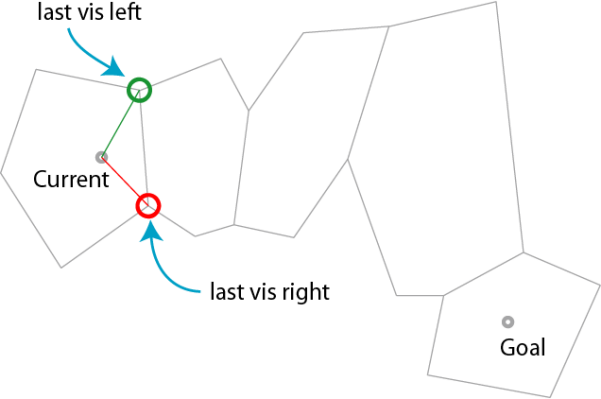
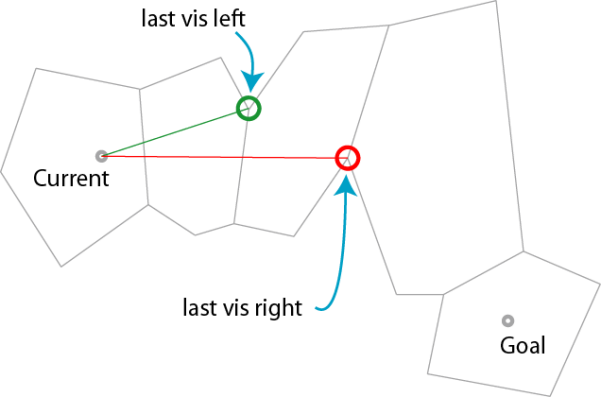
当最右的左边缘点与最右的左边缘点发生重叠时，此时该两边缘点中较早遇到的即是路径上的拐点。将起始位置置为该拐点，继续进行相同处理，直至找到路径上所有拐点。

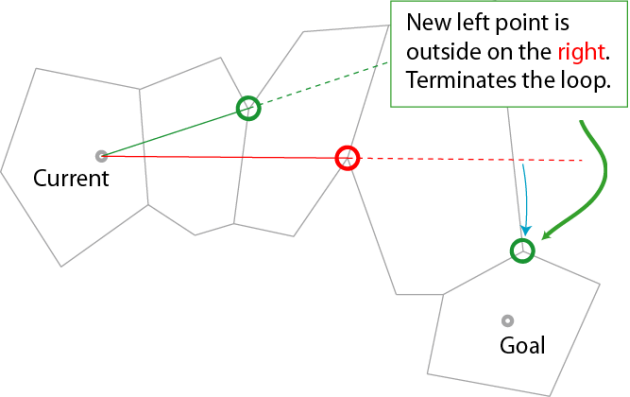
这里就结束了，科科。